Математики з Університету Монаша розв’язали 380-річну геометричну головоломку, запропоновану Декартом, розширивши його теорему про взаємно дотичні кола на конфігурації з довільною кількістю кіл.
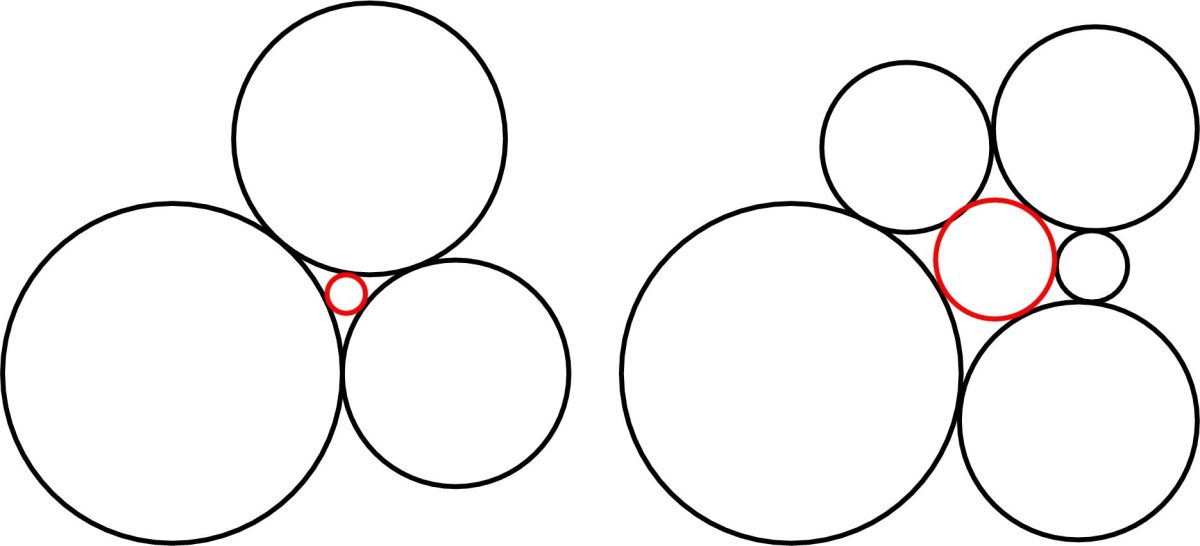
Дослідники доцент Деніел Метьюз та аспірант Оріон Зимаріс опублікували своє відкриття в Journal of Geometry and Physics. Їхнє дослідження пропонує загальне рівняння для конфігурацій дотичних кіл, відомих як “n-квіти”. Це досягнення має особливе значення, оскільки математики століттями намагалися узагальнити теорему Декарта на більшу кількість кіл. Відкриття подолало математичну загадку, що залишалася невирішеною з 17 століття.
Історичний контекст та методологія
Класична теорема Декарта виникла з проблеми, яку філософ запропонував принцесі Єлизаветі Пфальцській у 1643 році. “У 1643 році Декарт поставив перед принцесою Єлизаветою Пфальцською проблему, припускаючи, що зможе її розв’язати. Адже він щойно винайшов декартові координати! Але він не зміг, і коли він переробив проблему до практично розв’язуваної, це стало відомо як класична теорема Декарта про коло”, – пояснив доцент Метьюз.
Дослідники застосували сучасні математичні інструменти, зокрема спінори. Спінори – це “математичні об’єкти, що використовуються у квантовій механіці та теорії відносності”. Зимаріс відзначив неочікувані міждисциплінарні зв’язки у їхньому дослідженні. “Наш підхід використовував передові геометричні інструменти, натхненні фізикою, що було несподівано”, – зазначив він.
Міждисциплінарні зв’язки
Команда спиралася на спінори, розроблені лауреатом Нобелівської премії Роджером Пенроузом та Вольфгангом Ріндлером. “Виявляється, що ті самі математичні структури, які описують квантовий спін і теорію відносності, також допомагають нам зрозуміти пакування кіл”, – підкреслив Зимаріс. Ця робота демонструє, як фундаментальні математичні структури проявляються в різних галузях науки.
Відкриття не лише збагачує чисту математику, але й підкреслює зростаючу силу групи топології в університеті. Ця група тепер включає дев’ять аспірантів, п’ять з яких – жінки. “Це відкриття є чудовим прикладом того, як класичні проблеми можуть надихати нову математику через століття”, – підсумував доцент Метьюз.
